Magnetismus
Magnetismus ist ein physikalisches Phänomen, das sich unter Anderem als Kraftwirkung zwischen Magneten, magnetisierten bzw. magnetisierbaren Gegenständen und bewegten elektrischen Ladungen wie z. B. in stromdurchflossenen Leitern äußert. Die Vermittlung dieser Kraft erfolgt über ein Magnetfeld, das einerseits von diesen Objekten erzeugt wird und andererseits auf sie wirkt.
Magnetfelder entstehen zum einen bei jeder Bewegung von elektrischen Ladungen. Das ist Grundlage von Elektromagneten und wegen des Induktionsgesetzes auch der induktiven elektronischen Bauelemente. Zum anderen existiert das magnetische Moment von Elementarteilchen als Folge ihres Spins, was zu Dauermagneten und anderen magnetischen Eigenschaften von Festkörpern, aber auch Flüssigkeiten und Gasen führt.
Der Magnetismus ist ein Teilgebiet des Elektromagnetismus, welcher eine der vier Grundkräfte der Physik repräsentiert.

Magnetfelder und Feldlinien
Um die Erscheinungen des Magnetismus zu beschreiben, führte man den Begriff des Magnetfelds ein. Magnetfelder können verursacht werden durch
- magnetische Materialien, etwa einen Dauermagneten,
- elektrische Ströme, z. B. eine stromdurchflossene Spule oder
- zeitliche Änderung eines elektrischen Feldes.
Magnetische Feldlinien veranschaulichen in jedem Punkt des Feldes Richtung und Richtungssinn des Magnetfeldes bzw. des magnetischen Flusses. Der Abstand zwischen benachbarten Feldlinien ist ein Anhaltspunkt für die Stärke des Magnetfeldes: je dichter die Feldlinien, desto stärker das Feld.
Magnetische Feldlinien haben keinen Anfang und kein Ende, sondern verlaufen als geschlossene Bahnen.[1] In der Magnetostatik gibt es im Gegensatz zur Elektrostatik keine Ladungen – magnetische Monopole sind zwar denkbar, alle experimentellen Tatsachen sprechen aber gegen ihre Existenz. Somit ist das Magnetfeld quellenfrei. [2]
Magnetische Feldlinien können durch die Ausrichtung von Eisenfeilspänen oder einer Kompassnadel sichtbar gemacht werden; für dreidimensionale Demonstrationen kann man die Eisenfeilspäne zum Beispiel in Silikonöl suspendieren.
Hall-Sonden sind elektronische Sensoren auf Basis des Hall-Effektes, die Stärke und oft auch Richtung der Magnetfelder messen können.
Nord- und Südpol
Bei Elektromagneten oder Permanentmagneten bezeichnet man Gebiete, aus denen die Feldlinien austreten, als Nordpol und Gebiete, in die Feldlinien eintreten, als Südpol. Stabmagneten richten sich bei Fehlen anderer Kräfte so aus, dass der Nordpol in Richtung Norden, zum arktischen Magnetpol, und der Südpol in Richtung des antarktischen Magnetpols zeigt. Daher rührt auch der Name. Da der Nordpol vom arktischen Magnetpol angezogen wird, ist der Arktische Magnetpol ein magnetischer Südpol.
Magnetische Kraftwirkung
Das magnetische Feld übt eine Kraft auf bewegte Ladungen aus, die so genannte Lorentzkraft, Sie ist proportional zur Geschwindigkeit , wirkt senkrecht zu den Feldlinien des Magnetfeldes und senkrecht zur Bewegungsrichtung der Ladung. Sie ist die Grundlage vieler Generatoren sowie der Ablenkung bewegter geladener Teilchen (z. B. mit Ablenkspulen). Mit dem Magnetfeld wird dabei keine Energie ausgetauscht – es ist lediglich Vermittler (Anmerkung: bei solchen Generatoren und Motoren ist dies das Erregerfeld).
Das magnetische Feld übt ferner Kräfte auf Magnete und magnetisierbare Körper (Ferrimagnetismus bestimmter nichtmetallischer Festkörper, sog. Ferrite, und Ferromagnetismus von Metallen wie Eisen) aus. Magnete und gestreckte Probekörper aus magnetisierbaren Materialien richten sich immer längs der Feldlinien beziehungsweise antiparallel zu diesen aus, das heißt, der magnetische Südpol eines Probemagneten richtet sich entlang der Feldlinien zum Nordpol des erzeugenden Feldes aus. Dieser Effekt wird zum Beispiel beim magnetischen Kompass ausgenutzt, bei dem sich die Kompassnadel, ein magnetischer Dipol, nach dem Erdmagnetfeld ausrichtet. Weitere Beispiele sind Zugmagnete, Haltemagnete und Elektromagnete an Magnetkränen.
Da sich ungleichnamige Pole anziehen und gleichnamige abstoßen, sind zwei Magnete bestrebt, ungleichnamige Pole einander zuzuwenden. Handelt es sich jeweils um inhomogene, d. h. mit dem Ort variierende Felder, ziehen sich die beiden Magnete an. Ursache für beide Beobachtungen ist, dass ein energieärmerer Zustand eingenommen wird – die Kräfte wirken stets so, dass die Gesamtenergie des Feldes abnimmt, wenn die Magnete ihnen folgen. In der mathematischen Beschreibung der Kraft spielt daher der Gradient des Magnetfeldes eine Rolle.
Bei der Ausrichtung von Magneten und magnetisierbaren Körpern in Magnetfeldern wird Energie mit dem Feld ausgetauscht – folgen die Körper der Kraft, nimmt die Summe der Feldenergie ab, und es wird mechanische Arbeit frei. Werden die Magnete auseinandergezogen, muss mechanische Arbeit verrichtet werden, und dadurch steigt die Feldenergie des resultierenden Gesamtfeldes. Die Magnetisierung beteiligter Dauermagnete bleibt dabei jedoch erhalten. Sind magnetisierbare Körper umgebende Spulen beteiligt, kann auch Elektroenergie am Energieaustausch beteiligt sein. Beispiele hierfür sind Reluktanzmotoren und Schrittmotoren.
Größen und Einheiten
Die Stärke eines Magnetfeldes kann durch zwei verschiedene physikalische Größen ausgedrückt werden, die magnetische Feldstärke H (Einheit: A/m, also Ampère pro Meter; im CGS-Einheitensystem gibt es den Namen Oersted für die entsprechende Einheit) und die magnetische Flussdichte (die sog. „magnetische Induktion“) B (Einheit Tesla). Diese unterscheiden sich im Vakuum nur durch eine multiplikative Konstante . In Materie, z. B. in Permanentmagneten, ist der Zusammenhang komplizierter: In diesem Fall ist das in einem Querspalt (mit einer Magnetfeld-Sonde) gemessene Feld, während in einem Längsspalt zu messen ist und von wesentlich verschieden ausfallen kann. Die Größe ist immer quellenfrei, während das Gleiche für nicht gilt (s. u.). Während die magnetische Feldstärke bei Berechnungen mit elektrischen Strömen oder bei ferromagnetischem oder ferrimagnetischem Material von Vorteil ist, verwendet man die magnetische Flussdichte zum Berechnen von induzierten Spannungen oder der Lorentzkraft. Die beiden Feldgrößen sind über die Materialgleichungen der Elektrodynamik miteinander verknüpft, welche sich im einfachsten Fall über einen Faktor, die magnetische Permeabilität, ausdrücken lässt; im allgemeinen Fall gilt stattdessen wobei der Vektor als die sog. Magnetisierung des Materials bezeichnet wird. Quellenfreiheit von und Wirbelfreiheit von – letzteres nur im Falle der Abwesenheit elektrischer Ströme, – drücken sich mathematisch durch die Gleichungen bzw. aus. Dabei sind div bzw. rot die Quellen- bzw. Wirbeldichten des Feldes (siehe Divergenz bzw. Rotation).
Beispiele für Magnetfelder
Das intergalaktische Magnetfeld, ausgedrückt als magnetische Flussdichte in der Einheit Tesla (T), schätzt man auf weniger als 0,1 nT (10−10 T), das der Milchstraße auf 30 nT. Das Magnetfeld der Erde hat an der Oberfläche eine Stärke um 40 µT, dies entspricht im Gaußschen Einheitensystem 0,4 Gauss. Die magnetische Flussdichte der Sonnenflecken liegt unter 1 mT. Die Sättigungsmagnetisierung von Eisen beträgt ca. zwei Tesla.
Auf der Oberfläche von Neutronensternen, wie z. B. Pulsaren, herrschen dagegen typischerweise Flussdichten von 108 Tesla, bei Magnetaren, einer speziellen Sorte von Neutronensternen, sogar 1011 Tesla.
Das mit 1 nT derzeit (2009) schwächste Magnetfeld auf der Erde findet man in einem speziell abgeschirmten kubischen Gebäude der Physikalisch-Technischen Bundesanstalt in Berlin. Zweck des Kubus’ ist die Messung der schwachen Hirnströme von Menschen. Am National High Magnetic Field Laboratory in Tallahassee (Florida) wird das mit 45 T derzeit stärkste (stabile) Magnetfeld auf der Erde erzeugt.
Höhere Magnetfelder können mit Elektromagneten nur in kurzen Pulsen erzeugt werden. Den Weltrekord für zerstörungsfreie Magnetbauweisen hält derzeit (2012) das National High Magnetic Field Laboratory in Los Alamos, USA mit 100,75 T.[3] Mittels intensiver Laserstrahlung lassen sich Flussdichten von bis zu 34 Kilotesla erzeugen – allerdings nur für die sehr kurze Zeitspanne von etwa 10 ps. Solch hohe Magnetfelder (beispielsweise 2800 T[4]) lassen sich in gepulsten Anordnungen erzeugen, wenn in Kauf genommen wird, dass der Magnet dabei zerstört wird (bzw. sich selbst zerstört).
Magnetische Energie
Jedes Magnetfeld enthält Energie. Die Energiedichte an einem beliebigen Punkt eines Magnetfelds im Vakuum ist gegeben durch
- .
Dabei ist der Betrag der magnetischen Flussdichte am gegebenen Punkt und die Permeabilität des Vakuums.
Die Gesamtenergie des Magnetfelds einer stromdurchflossenen Spule beträgt
- .
Hier steht für die Induktivität der Spule und für die Stromstärke.
Elektromagnetismus
Bei magnetischen Feldern handelt es sich um einen Effekt, der durch die Relativbewegung zwischen geladenen Teilchen entsteht. Er wird durch die Spezielle Relativitätstheorie beschrieben bzw. bei Berücksichtigung quantenmechanischer Effekte („Spinmagnetismus“ u. a.) durch die relativistische Quantenmechanik von Paul Dirac.
Ersetzt man etwa einen stromdurchflossenen Draht als typische Ursache eines Magnetfelds durch einen dünnen isolierenden, in longitudinaler Richtung magnetisierten Permanentmagneten, so gilt außerhalb des Drahtes aber man beobachtet trotzdem quantenmechanische Interferenzen (siehe Aharonov-Bohm-Effekt), was zeigt, dass außer der Elektrodynamik auch die Quantenmechanik eine wesentliche Rolle bei der Erklärung der magnetischen Phänomene spielt. Für eine abstraktere Darstellung und Einordnung des Elektromagnetismus siehe den Artikel Elektromagnetische Wechselwirkung.
Bewegungen von Ladungsträgern bewirken Veränderungen im elektrostatischen und magnetischen Feld ihrer Umgebung. Da sich diese Veränderungen im Raum ausbreiten, spricht man von elektromagnetischen Wellen. Licht (egal ob sichtbar oder unsichtbar) und Rundfunk sind die bekanntesten Formen dieses Prinzips, aber auch in der Metallverarbeitung (Induktionsöfen) und zum Erhitzen sogar nichtleitender Substanzen kommt diese Form des Elektromagnetismus zur Anwendung (Mikrowellenherd).
Richtungsregeln
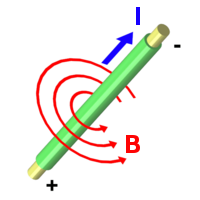
Betrag und Vorzeichen der bewegten Ladungen sowie Betrag und Richtung ihrer Geschwindigkeit bestimmen die Stärke und Richtung der magnetischen Kräfte sowie der ihnen zugrundeliegenden magnetischen Felder, deren exakte Messung heute u. a. mit Hall-Sonden möglich ist.
Für den Zusammenhang zwischen Stromrichtung und Richtung der magnetischen Kräfte bzw. der ihnen zugrundeliegenden magnetischen Felder ist dabei eine Reihe unterschiedlich bezeichneter Regeln und Merkhilfen im Umlauf, die sich zunächst einmal danach unterscheiden, ob bei ihnen von der „konventionellen“ bzw. „technischen“ Stromrichtung (entgegen dem Elektronenfluss) oder aber der Richtung des Elektronenflusses (umgangssprachlich auch „physikalische“ Stromrichtung genannt) ausgegangen wird. Ist ersteres der Fall, spricht man von Rechte-Hand- oder Rechte-Faust-Regeln, ansonsten von Linke-Hand- oder Linke-Faust-Regeln, wobei die zuerst genannten traditionell vorherrschen.
Die nächste Unterscheidung ist die danach, ob man sich bei der betreffenden Regel außer dem Daumen auch des jeweils im rechten Winkel zum Vorgänger abgespreizten Zeige- und Mittelfingers bedient oder aber sich alle Finger außer dem Daumen zu einer Faust geschlossen vorstellt.
Während die zuerst genannten Regeln damit als eigentliche Linke- bzw. Rechte-Hand-Regeln – auch Drei-Finger-Regel, UVW-Regel oder IBF- bzw. FBI-Regel genannt – die Richtung der Lorentzkraft auf einen bewegten Ladungsträger in einem (vorgegebenen) äußeren Magnetfeld anzeigen, dienen die an zweiter Stelle genannten Regeln – Linke- bzw. Rechte-Faust-Regel, Umfassungsregel, populär auch Schraubenregel bzw. Korkenzieherregel genannt – in erster Linie dazu, die Richtung des Magnetfeldes anzuzeigen, das der bewegte Ladungsträger durch seine Bewegung selbst erzeugt, sei es frei fliegend oder aber in einem geradlinigen bzw. ringförmigen elektrischen Leiter, z. B. einer Spule.
Beispiele: Rechte-Hand-Regel bzw. (rechtshändige) UVW-Regel
- Zeigt der abgespreizte Daumen der rechten Hand in die konventionelle bzw. technische Stromrichtung eines stromdurchflossenen (Ursache) Leiters und der im rechten Winkel zum Daumen abgespreizte Zeigefinger in Richtung des äußeren Magnetfelds (Vermittlung), weist der im rechten Winkel zu beiden abgespreizte Mittelfinger in Richtung der auf die Ladungsträger im Leiter (und damit ihn selbst) wirkenden Lorentzkraft (Wirkung).
- Und umgekehrt: Wird ein elektrischer Leiter durch mechanische Bewegung (Ursache) in Richtung des abgespreizten Daumens der rechten Hand in ein äußeres Magnetfeld (Vermittlung) gebracht, dessen Richtung die des im rechten Winkel zum Daumen abgespreizten Zeigefingers ist, so wird in dem Leiter ein Stromfluss (Wirkung) in Richtung des zu beiden abgespreizten Mittelfingers induziert.
Beispiele: Rechte-Faust-Regel bzw. Korkenzieherregel
- Wird ein stromdurchflossener Leiter mit der rechten Hand so umfasst, dass der abgespreizte Daumen in Richtung der konventionellen bzw. technischen Stromrichtung weist, zeigen die gekrümmten Finger in Richtung des entstehenden Magnetfeldes.
- Für einen Kreisstrom (z.B. den einer Spule) gilt dementsprechend: Wird die Spule mit der rechten Hand so umfasst, dass die Finger in Richtung der technischen Stromrichtung gekrümmt sind, zeigt der abgespreizte Daumen in Richtung des magnetischen Nordpols.
Erklärung des Phänomens
Beim Magnetismus handelt es sich (ähnlich wie bei der Supraleitung) um spezifisch-quantenmechanische Effekte, die nicht einfach darzustellen sind. Ein erfolgreiches Modell wurde schon 1927 mit der Heitler-London-Theorie der Bildung von Wasserstoff-Molekülen entwickelt, obwohl diese Theorie zunächst nichts mit „Magnetismus“ zu tun zu haben schien. Nach dieser Theorie entstehen sog. σ-Molekülorbitale, d. h. es bildet sich aus den zwei atomaren Wasserstoff-Funktionen ui(…) ein orbitaler sogenannter σ-Molekülzustand:
Das letzte Produkt ergibt sich aus dem ersten wegen des quantenmechanischen Prinzips der Ununterscheidbarkeit identischer Teilchen. Es bedeutet: Das erste Elektron, r1, kann sich nicht nur beim ersten Atomkern befinden, sondern ebenso gut in einem atomaren Wasserstoff-Orbital beim zweiten Atomkern, während sich das zweite Elektron beim ersten Atomkern befindet. Dies ergibt die sogenannte „Austauschwechselwirkung“, die für das Zustandekommen des Magnetismus eine fundamentale Rolle spielt und um Faktoren von 100 bis 1000 stärker ist als die durch die Elektrodynamik beschriebenen phänomenologischen Terme.
Bei der Spinfunktion χ(s1, s2), welche für den Magnetismus verantwortlich ist, gilt dann wegen des sogenannten Pauli-Prinzips das komplementäre Verhalten [5]
d. h. es müssen nicht nur die ui durch α und β ersetzt werden (ersteres bedeutet „spin up“, letzteres „spin down“), sondern auch + durch −, sowie z. B. r1 durch die beiden diskreten Werte von s1, nämlich durch ±½. Und zwar gilt (+1/2)= (-1/2) = 1 und (-1/2)= (+1/2) = 0. Es ergibt sich so, d. h. mit dem Minuszeichen in (1b), eine Singulett-Spinfunktion. Das besagt: die Spins sind antiparallel; beim Festkörper bedeutet das Antiferromagnetismus und bei zweiatomigen Molekülen Diamagnetismus. Die Tendenz zur Molekülbindung, entsprechend der oben angegebenen Ortsfunktion, ergibt also wegen des Pauli-Prinzips automatisch die schon erwähnte Singulettsymmetrie des Spinzustandes; wogegen die Coulomb-Abstoßung der beiden Elektronen zu einer Singulett-Ortsfunktion und komplementär dazu zu einer Triplett-Spinfunktion führen würde, d. h. „die Spins würden jetzt parallel stehen“. Der letztgenannte Effekt überwiegt bei Eisen, Kobalt und Nickel; diese Metalle sind ferromagnetisch. Bei den zweiatomigen Molekülen überwiegt er auch beim Sauerstoff, das im Gegensatz zu den anderen zweiatomigen Molekülen nicht diamagnetisch, sondern paramagnetisch ist. Der zuerst genannte Effekt überwiegt dagegen bei den anderen Metallen wie Natrium, Kalium, Magnesium oder Strontium, die nichtmagnetisch sind, oder bei Mangan, das antiferromagnetisch ist.
Aus dem Heitler-London-Modell entstand durch Verallgemeinerung das grundlegende sogenannte Heisenberg-Modell des Magnetismus [6] (Heisenberg 1928).
Die Erklärung des Phänomens beruht also letztlich auf allen Subtilitäten der Quantenmechanik, einschließlich ihrer mathematischen Struktur, insbesondere auf dem dort beschriebenen Spin und dem Pauli-Prinzip, während die Elektrodynamik eher die Phänomenologie beschreibt.
Magnetismus der Materie
Magnetisches Moment von Elementarteilchen
Viele geladene Elementarteilchen besitzen ein charakteristisches magnetisches Moment . Es ist über das gyromagnetische Verhältnis mit ihrem Spin verknüpft.
| Elementarteilchen | Bezeichnung | |
|---|---|---|
| Elektron | ||
| Myon | ||
| Proton | ||
| Neutron |
Magnetisches Moment von Atomen
Das magnetische Moment eines Atoms setzt sich zusammen aus dem Beitrag der Elektronenhülle (Hüllenmoment) und dem im Allgemeinen viel schwächeren Kernbeitrag (Kernmoment).
Zum Hüllenmoment tragen das Bahnmoment, das mit dem Bahndrehimpuls der Elektronen verknüpft ist, und das durch den Elektronenspin bestimmte Spinmoment bei. Die Summe der magnetischen Momente der Elektronen eines doppelt besetzten Orbitals ergibt jeweils null, sodass Atome, die keine halbbesetzten Orbitale besitzen, kein permanentes Hüllenmoment aufweisen.
Das Kernmoment ist zwar sehr klein, es lässt sich aber dennoch nicht nur nachweisen (Zeeman-Effekt, Stern-Gerlach-Versuch), sondern auch praktisch anwenden (z. B. NMR-Spektroskopie (Nuclear Magnetic Resonance, kernmagnetische Resonanz), MR-Tomographie).
Magnetismus von Festkörpern
Magnetismus von Festkörpern ist ein kooperatives Phänomen. Die makroskopische Magnetisierung setzt sich additiv zusammen aus den Beiträgen der einzelnen Bausteine (Atome, Ionen, quasifreie Elektronen), aus denen der Festkörper aufgebaut ist. Bei vielen Materialien haben bereits die einzelnen Bausteine ein magnetisches Moment. Allerdings weisen selbst von den Materialien, deren Bausteine nichtverschwindende magnetische Momente tragen, nur wenige eine makroskopische Magnetisierung auf. Dies geschieht dann, wenn sich die einzelnen Bausteine so anordnen, dass sich ihre Beiträge nicht aufheben.
In Festkörpern können fünf Typen von Magnetismus auftreten.[8] Ihre Namensgebung erfolgt beim magnetischen wie auch beim elektrischen Feld durch die Verwendung der entsprechenden Vorsilbe ganz analog:
| Magnetismus | Erklärung | Veranschaulichung |
|---|---|---|
| Diamagnetismus | Bringt man eine Substanz in ein magnetisches Feld, so induziert dieses in den Elektronenhüllen der Atome einen Strom, dessen Magnetfeld nach der Lenzschen Regel dem äußeren entgegengerichtet ist. Diamagnetismus führt so zu einer Abschwächung des Magnetfeldes in der Substanz. In Materialien deren Atome, Ionen oder Moleküle keine ungepaarten Elektronen besitzen, ist Diamagnetismus die einzige Form von Magnetismus. | |
| Paramagnetismus | Besitzen die Atome, Ionen oder Moleküle eines Materials ein magnetisches Moment, so richten sich diese parallel zum äußeren Magnetfeld aus. Dies bewirkt eine Verstärkung des Magnetfeldes im Material. Bei einem idealen Paramagneten sind die einzelnen magnetischen Momente voneinander isoliert. Darum bricht das innere Magnetfeld nach Entfernen des äußeren Magnetfelds wegen der Wärmebewegung der Teilchen zusammen. Dementsprechend nimmt der Paramagnetismus mit steigender Temperatur ab. | |
| Ferromagnetismus | Beim Ferromagnetismus sind die magnetischen Momente einzelner Teilchen nicht unabhängig voneinander, sondern richten sich spontan parallel aus. Die Kopplung der magnetischen Momente erstreckt sich aber nicht über das ganze Material sondern ist auf kleine Bereiche, die Weissschen Bezirke, beschränkt. Typische Längenskalen sind 10 Nanometer bis wenige Mikrometer. Die Ausrichtung der Weissschen Bezirke ist statistisch verteilt, so dass der Gesamtkörper unmagnetisch erscheint. Durch ein äußeres Magnetfeld kann man die Bezirke gleichrichten. Diese Gleichrichtung bleibt auch nach Entfernen des äußeren Feldes erhalten, so dass man eine permanente Magnetisierung erhält. Die Magnetisierung kann durch Erhitzen über die ferromagnetische Curie-Temperatur zerstört werden. | |
| Ferrimagnetismus | Auch beim Ferrimagnetismus sind die magnetischen Momente einzelner Teilchen nicht unabhängig voneinander. Es liegen aber zwei Arten von magnetischen Zentren vor. Die Spinmomente gleichartiger Zentren richten sich dabei parallel und die verschiedener antiparallel aus. Dieses führt zu einer partiellen Auslöschung der magnetischen Momente. Im übrigen Verhalten ähneln sie den Ferromagneten. | |
| Antiferromagnetismus | Auch beim Antiferromagnetismus sind die magnetischen Momente einzelner Teilchen nicht unabhängig voneinander sondern richten sich spontan antiparallel aus. Daher zeigt der ideale Antiferromagnet nach außen kein magnetisches Verhalten. Mit steigender Temperatur stört die Wärmebewegung die Anordnung, so dass sich der Antiferromagnet zunehmend wie ein Ferrimagnet verhält. Bei Erhitzen über die Néel-Temperatur verhält sich der Antiferromagnet nur noch paramagnetisch (vergleiche Curie-Temperatur beim Ferromagneten). | 
|
Darüber hinaus gibt es noch weitere Sonderformen des Magnetismus, die durch nicht magnetisches oder nichtlineares Verhalten der fünf Magnetismustypen geprägt sind:
- Amagnetismus
- Ein amagnetischer Stoff ist im Allgemeinen unbeeinflussbar durch magnetische Felder. Häufig findet man auch die Bezeichnungen nicht- oder unmagnetisch. Zu beachten ist jedoch, dass es bei sehr hohen Magnetfeldstärken auch bei amagnetischen Materialien zu Anziehungs- oder im noch geringeren Maße zu Abstoßungseffekten kommen kann. Diese Effekte sind jedoch wesentlich schwächer als es zum Beispiel bei ferromagnetischen Stoffen (wie z. B. Eisen) der Fall wäre. Die Bezeichnung amagnetisch ist nicht einheitlich, und der Grad des Magnetismus kann beobachtbar schwanken.
- Metamagnetismus
- Metamagnetische Materialien (z. B. Eisen(II)-chlorid) weisen bei sehr kleinen äußeren Magnetfeldern verschwindend kleine Magnetisierungen auf (antiferromagnetisch), bei größer werdender Feldstärke nimmt die Magnetisierung unverhältnismäßig stark und gleichbleibend zu, und geht gegen einen Sättigungswert. Dieses Verhalten lässt sich darin begründen, dass sich der Kristall für kleine Felder antiferromagnetisch, und für starke Felder ferromagnetisch verhält.[9]
Magnetismus in der Biologie
Weil jede Nervenaktivität auch aus elektrischen Strömen besteht, produziert unser Nervengewebe und insbesondere unser Gehirn ständig Magnetfelder, die mit empfindlichen Detektoren empfangen werden können.
Magnetische Wechselfelder können über Induktion elektrische Ströme im Gewebe auslösen und können so einen (schwachen) Einfluss auf das Nervensystem haben. So kann der motorische Cortex derartig mit Hilfe der Transkraniellen Magnetstimulation (TMS) stimuliert werden, dass es zu unwillkürlichen Muskelkontraktionen kommt. Auch die Nerven in den Muskeln selbst können auf diese Weise stimuliert werden.
In entsprechend starken Feldern (zum Beispiel in einem Kernspintomograf) treten sogenannte Magnetophosphene (optische Sinneswahrnehmungen) auf. Des Weiteren ist seit langem bekannt, dass magnetische Wechselfelder die Sekretion von Hormonen (Beispiel Melatonin) beeinflussen können.
Viele Vögel, Meeresschildkröten und weit ziehende Fische verfügen über einen Magnetsinn und können sich mittels des Erdmagnetfelds orientieren.
Der Arzt Franz Anton Mesmer entwickelte eine Theorie, die 1784 von der französischen Akademie der Wissenschaften geprüft und verworfen wurde, nach der ein Fluid, das Mesmer als Magnetismus animalis bezeichnete, von Mensch zu Mensch übertragbar sei und bei der Hypnose und bestimmten Heilverfahren (Mesmersche Streichungen) eine Rolle spielen sollte.
Siehe auch: Magnetotaxis, Magnetospirillum magnetotacticum, Magnetosom
Gefahren
Wirkungen oder Gefahren magnetischer Gleichfelder auf den Menschen sind nicht bekannt. Auch die gepulsten Felder bei der Kernspintomografie sind ungefährlich. Dagegen kommt es bei starken Feldern in folgenden Fällen zu Gefahren:
- Kraftwirkung durch an oder im Körper vorhandene ferri- oder ferromagnetische Teile
- umher fliegende ferri- oder ferromagnetische Teile
Daher gelten in Magnetfeldlaboren und an Kernspintomografen Sicherheitsregeln, die gewährleisten, dass keinerlei magnetische Teile in die Nähe geraten. Folgende Schäden sind weiterhin relevant:
- Störung oder Ausfall von Herzschrittmachern
- Störung nicht „amagnetischer“ Uhren und anderer mechanischer Geräte
Gepulste Felder können durch elektromagnetische Induktion sämtliche elektronischen und elektrischen Einrichtungen beeinflussen oder zerstören, vgl. auch Elektromagnetischer Puls.
Der sporadisch starke Teilchenstrom der Sonne (Sonnenwind) führt auf der Erde zu sogenannten magnetischen Stürmen, die durch Induktion Telefon- und Überlandleitungen sowie Kabelsysteme und metallene Versorgungsleitungen gefährden.
Durch magnetische Felder werden magnetische Datenträger (Tonband, Festplatte) gelöscht.
Wenn ein Magnetfeld als Folge eines Zwischenfalls – Kurzschluss beim konventionellen Elektromagneten oder Quenchen beim Supraleitungsmagneten – schlagartig zusammenbricht, können durch Induktion sehr hohe elektrische Spannungsimpulse entstehen. Führen diese zu Stromfluss, können die dadurch wiederum erzeugten Magnetfelder z. B. Gegenstände gewaltsam in den Magneten hineinziehen. Daher dürfen Experimentieraufbauten in direkter Nähe des Magneten keine geschlossenen Leiterschleifen – beispielsweise in irgendwelchen Gestellen – enthalten; dies wird durch Einfügen isolierender Zwischenstücke erreicht.
Magnetismus in Umgangssprache und Alltag
Unter Magnetismus wird in der Umgangssprache praktisch ausschließlich der Ferromagnetismus verstanden. Der Ferromagnetismus ist ein im Alltag häufig vorkommendes und praktisch begreifbares Phänomen: Haftmagnete auf der Pinnwand, Kompass, uvm. Die anderen Arten des Magnetismus (Diamagnetismus, Paramagnetismus, usw.) sind dagegen eher exotische Laborphänomene.
Die meisten Menschen verbinden den Begriff Magnetismus richtigerweise sehr stark mit den Werkstoffen Eisen und Stahl. Weniger bekannt ist, dass auch Nickel und Kobalt ferromagnetisch sind. Für Überraschungen sorgt gelegentlich die Tatsache, dass viele Edelstähle nicht ferromagnetisch sind, obwohl sie zum großen Teil aus den ferromagnetischen Elementen Eisen und Nickel bestehen.
Zu Missverständnissen kommt es öfter durch die Verwechslung der Begriffe magnetisch, magnetisiert und magnetisierbar. Ein beliebiger Gegenstand aus einfachem Stahl ist magnetisch, dies bedeutet aber nicht, dass der Gegenstand auch magnetisiert ist. Ob ein Gegenstand magnetisch ist, kann man leicht prüfen, indem man ihn mit einem Dauermagneten berührt. Spürt man dabei eine Kraft, dann ist der Gegenstand ferromagnetisch. Ob ein Gegenstand magnetisiert ist – das heißt, dass der Gegenstand selbst die Eigenschaft eines Dauermagneten hat – ist schwieriger zu prüfen, vor allem wenn die Magnetisierung nur schwach ist. Man kann mit dem Gegenstand ein sehr leichtes Teil aus Stahl (z. B. eine Heft- oder Tackerklammer) berühren. Bleibt die Heftklammer an dem Gegenstand hängen, dann ist der Gegenstand magnetisiert. Eine solche Magnetisierung kann in der Praxis erwünscht sein (z. B. sind manche Schraubendreher absichtlich magnetisiert, damit die Handhabung kleiner Schrauben vereinfacht wird). Die Magnetisierung kann aber auch unerwünscht sein, weil man dadurch ständig kleine Stahlsplitter an dem Gegenstand hat.
Oft gibt es falsche Vorstellungen über die Magnetisierbarkeit. Laut verschiedenen Quellen lässt sich z. B. aus jedem beliebigen Stahldraht durch Überstreichen mit einem Dauermagneten eine provisorische Kompassnadel herstellen. In Wirklichkeit ist aber ein sehr weicher Stahldraht nicht gut geeignet, um daraus eine Kompassnadel herzustellen, weil weicher Stahl kaum magnetisierbar ist. Wenn man einen weichen Stahldraht mit einem Dauermagneten berührt, dann wird er zwar angezogen, aber nicht dauerhaft magnetisiert. Eine gehärtete Stahlnadel lässt sich dagegen dauerhaft magnetisieren und könnte damit als Behelfskompass funktionieren.
Siehe auch
Weblinks
- Magnetismus sehr ausführlich bei Welt der Physik
Einzelnachweise und Kommentare
- ↑ Mathematisch ausgedrückt: Magnetfelder sind stets Wirbelfelder, während elektrostatische Felder stets Gradientenfelder sind (man kann jedes Vektorfeld in einen Gradientenanteil (wirbelfreien Anteil) und einen Wirbelanteil (quellenfreien Anteil) aufspalten).
- ↑ Die Quellenfreiheit gilt - genau genommen - immer für die magnetische Flussdichte , nicht aber für die magnetische Feldstärke , siehe unten
- ↑ Magnetic field researchers target Hundred-Tesla goal, Pressemitteilung des Los Alamos National Laboratory vom 22. März 2012
- ↑ Präsentation der TU Dresden (pdf-Datei, 8,2 MB, abgerufen am 30. Juni 2011)
- ↑ Nach dem Pauli-Prinzip besteht die Komplementarität darin, dass bei zweiatomigen Molekülen eine symmetrische Ortsfunktion (Vorzeichen +) mit einer antisymmetrischen Spinfunktion (Vorzeichen −) zu multiplizieren ist, und umgekehrt.
- ↑ Zur Theorie des Magnetismus siehe z. B. U. Krey, A. Owen, Basic Theoretical Physics - A Concise Overview, Springer, Berlin 2007.
- ↑ Atomic and nuclear constants. In: NIST Standard Reference Database 121. NIST, Oktober 2008, abgerufen am 12. April 2009 (englisch).
- ↑ Arnold Fr. Holleman, Egon Wiberg: Lehrbuch der Anorganischen Chemie. 101. Auflage. Gruyter, New York, Berlin 1995, ISBN 3-11-012641-9, S. 1300–1310.
- ↑ Gerhard Fasching: Werkstoffe für die Elektrotechnik. 3. Auflage. Springer, Wien 1994, S. 384.