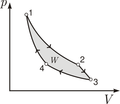
Adiabatische Zustandsänderung

Eine adiabatische Zustandsänderung (gr. α a „nicht“ und διαβαίνειν diabaínein „hindurchgehen“) ist ein thermodynamischer Vorgang, bei dem ein System von einem Zustand in einen anderen überführt wird, ohne thermische Energie mit seiner Umgebung auszutauschen.

Bedeutung

Im Allgemeinen kann ein thermodynamisches System seine innere Energie $U$ verändern, indem es sowohl (mechanische oder anders geartete) Arbeit $δ W$ als auch Wärme $δ Q$ mit seiner Umgebung austauscht. Nach dem ersten Hauptsatz der Thermodynamik gilt dabei für ein geschlossenes System, wenn äußere Energien (kinetische und potentielle) außer Betracht bleiben können:

d U = δ Q + δ W .

Bei einer adiabatischen Zustandsänderung findet kein Wärmeaustausch mit der Umgebung statt ( $δ Q = 0$ ), so dass die gesamte am System verrichtete Arbeit vollständig in die innere Energie übergeht oder ein Teil der inneren Energie vollständig in Arbeit umgewandelt wird, die vom System geleistet wird:

d U = δ W

(Erster Hauptsatz für ein adiabates, geschlossenes und ruhendes System).

Berechnungen und theoretische Überlegungen können dadurch stark vereinfacht oder unter Umständen erst ermöglicht werden.

Es sind sowohl irreversibel als auch reversibel ablaufende adiabatische Zustandsänderungen möglich. Im ersten Fall wird im System während des Vorgangs Entropie erzeugt, im letzten Fall nicht. Weil keine Wärmeenergie mit der Umgebung ausgetauscht wird, fließt auch keine Entropie zu oder ab. Ist die Zustandsänderung reversibel, so bleibt die Entropie des Systems daher gleich, es handelt sich dann um eine isentrope Zustandsänderung. (Das Umgekehrte gilt nicht: eine isentrope Zustandsänderung kann auch irreversibel und nicht-adiabatisch sein, wenn exakt die erzeugte Entropie nach außen abfließt; ein weiteres Gegenbeispiel ist das Verhalten bei Annäherung an den absoluten Temperaturnullpunkt: Hier sind die Zustandsänderungen wegen des 3. Hauptsatzes der Thermodynamik (fast) immer isentropisch, aber nur in Ausnahmefällen adiabatisch).

Reversible adiabatische Zustandsänderungen spielen ferner eine wichtige Rolle bei der axiomatischen Begründung der Thermodynamik nach Carathéodory. Ausgehend von dem Axiom „Es gibt in der Nähe jedes reversibel erreichbaren Zustandes Zustände, welche nicht adiabatisch-reversibel, also nur irreversibel oder überhaupt nicht erreichbar sind“^[1] wird die Existenz einer neuen Zustandsgröße Entropie bewiesen. Zustände, zwischen denen nur irreversible Übergänge möglich sind, unterscheiden sich nämlich in ihrer Entropie, so dass kein adiabatisch-reversibler (also isentroper) Übergang zwischen ihnen existieren kann.

Näherungsweise Realisierung

Vorgänge in einer Thermoskanne laufen näherungsweise adiabatisch ab.

Eine ideale adiabatische Zustandsänderung setzt voraus, dass das System, in dem die Zustandsänderung stattfindet, perfekt gegen Wärmeströme jeglicher Form isoliert ist. Es wären also Wärmeleitung, konvektive Wärmeübertragung und Strahlungsaustausch vollständig zu unterbinden. Das System darf von einem Wärmestrom durchflossen werden, sofern keine Wärme daraus im System verbleibt; der Wärmestrom kann dann als nicht zum System gehörig betrachtet werden (Beispiele: ein völlig transparentes von der Sonne beschienenes System, ein von nicht wechselwirkenden Neutrinos durchflutetes System).

In der Realität ist eine vollständige Wärmeisolation nicht erreichbar, aber reale Vorgänge können in guter Näherung adiabatisch ablaufen, wenn

sie in einem gut isolierten Behälter stattfinden (z. B. chemische Reaktionen in einem adiabatischen Kalorimeter),
die Zustandsänderung so schnell verläuft, dass in der kurzen Zeit wenig Wärme zu- oder abfließen kann (z. B. in einem Verbrennungsmotor, beim Wiedereintritt von Raumflugkörpern oder bei einer Luftpumpe) oder
das Volumen des Systems sehr groß ist, so dass Wärmeströme an seinem Rand praktisch keine Rolle spielen (z. B. bei thermisch aufsteigenden Luftpaketen).

In der Realität handelt es sich praktisch immer um zumindest partiell diabatische Prozesse, so dass man nur noch näherungsweise von einer adiabatischen Zustandsänderung ausgehen kann.

Beispiele

Eine Cumulonimbuswolke

Nebelbildung im Unterdruckbereich der Tragflächen eines Flugzeuges

Eine F/A-18 Hornet im Überschallflug mit Wolkenscheibeneffekt

Die Kompression der Luft in einer Luftpumpe ist eine adiabatische Zustandsänderung. Wenn die Kompression mit genügend hoher Geschwindigkeit durchgeführt wird, ist eine deutliche Temperaturerhöhung spürbar. Die Arbeit, die an der Pumpe verrichtet wird, erhöht direkt die innere Energie und damit die Temperatur des Luftgemisches. Dabei wird zuerst keine Wärmeenergie an die Pumpe abgegeben bzw. von ihr aufgenommen. Erst nach Vollendung des Prozesses merkt man eine Erwärmung der Fahrradpumpe und damit einen Fluss der Wärmeenergie. Ein pneumatisches Feuerzeug nutzt dieses Verfahren. Auch die extrem schnelle primäre Erhitzung der Luft beim Wiedereintritt von Raumflugkörpern ist auf Grund der extrem hohen Verdichtungsgeschwindigkeiten ein näherungsweise adiabatischer Prozess. Allerdings verteilt sich die Wärme im Anschluss danach sehr schnell durch Leitungs-, Strömungs- und Strahlungsprozesse.
Umgekehrt zur Kompression verursacht ein adiabatischer Druckabfall eine Abkühlung der Luft. Dies geschieht zum Beispiel innerhalb eines aufsteigenden Luftstromes (bei thermischem Auftrieb oder beim Überströmen eines Gebirges) oder auch auf der Oberseite von Flugzeugtragflächen. Beim Abkühlen verringert sich die Sättigungskonzentration für Wasserdampf. Unterschreitet diese den tatsächlichen Wassergehalt, kondensiert der darüber liegende Wasseranteil zu kleinen Wassertröpfchen (Bildung von Wolken oder Nebel).

Arbeit bei einer reversiblen adiabaten (isentropen) Zustandsänderung eines idealen Gases

Im Falle eines idealen Gases gilt für die innere Energie:

U = N \frac{f}{2} k_{B} T

Wegen $f = \frac{2}{κ - 1}$ folgt:

U = \frac{N}{κ - 1} k_{B} T = \frac{\frac{N}{N_{A}}}{κ - 1} N_{A} k_{B} T = \frac{n R}{κ - 1} T

.

Hierbei bezeichnen N die Anzahl der Gasteilchen, f die Anzahl der nicht eingefrorenen Freiheitsgrade, $k_{B}$ die Boltzmann-Konstante, T die absolute Temperatur, $κ$ den Isentropenexponenten, n die Stoffmenge (in Mol), N_A die Avogadro-Konstante und R die allgemeine Gaskonstante.

Damit gilt wegen $δ W = d U$ für die bei einer reversiblen adiabatischen (isentropen) Zustandsänderung geleistete Arbeit (Volumenarbeit):

Δ W = \frac{n R}{κ - 1} Δ T = \frac{- n R}{κ - 1} (T_{1} - T_{2}) = \frac{- p_{1} V_{1}}{κ - 1} (1 - \frac{T_{2}}{T_{1}})

= \frac{- p_{1} V_{1}}{κ - 1} [1 - {(\frac{V_{1}}{V_{2}})}^{κ - 1}] = - n c_{v} (T_{1} - T_{2})

.

Hierbei bezeichnen $T_{1}, V_{1}$ die Anfangstemperaturen bzw. -volumina und $T_{2}, V_{2}$ die Endtemperaturen bzw. -volumina und $c_{v}$ die molare spezifische Wärme bei konstantem Volumen.

Daraus ergibt sich auch, dass die Arbeit des Prozesses mit höherer Temperaturdifferenz $T_{1} - T_{2}$ größer wird. Dies hat unter anderem den Temperaturgradienten der unteren Erdatmosphäre zur Folge.

Aus der Zustandsgleichung eines idealen Gases folgen diese Zusammenhänge:

p_{1} V_{1}^{κ} = p_{2} V_{2}^{κ}

\frac{T_{1}}{T_{2}} = {(\frac{V_{2}}{V_{1}})}^{κ - 1}

\frac{T_{1}}{T_{2}} = {(\frac{p_{1}}{p_{2}})}^{\frac{κ - 1}{κ}}

Diese Gleichungen lassen sich so umformen, dass gilt:

p V^{κ} = {const}_{1}

T V^{κ - 1} = {const}_{2}

T^{κ} p^{1 - κ} = {const}_{3}

Sie werden auch Poissonsche Gleichungen genannt. $κ$ ist hierbei der Isentropenexponent. Die Gleichungen können in dieser Form allerdings nur für dimensionslose Größen verwendet werden, z.B., wenn sie auf die Größen im Normzustand bezogen sind.

Da auch die Masse des Gasvolumens konstant bleibt, ist auch die Umformung auf die Änderung der Dichte einfach berechenbar:

ρ_{1} = ρ_{2} {(\frac{p_{1}}{p_{2}})}^{\frac{1}{κ}}

Isentropengleichung

Die allgemeine Isentropengleichung für dimensionslose Größen (s.o) lautet:

p \cdot V^{κ} = const .,

wobei $κ = \frac{C_{p}}{C_{v}} = \frac{f + 2}{f}$ gilt. Dabei ist $\frac{C_{p}}{C_{v}}$ das Verhältnis der isobaren und der isochoren Wärmekapazität und f bezeichnet die Zahl der Freiheitsgrade des Gases. Für ein ideales einatomiges Gas ergibt sich mit $f = 3$ und aus $C_{p} = \frac{5}{2} N k$ und $C_{V} = \frac{3}{2} N k$ für den Isentropenindex $κ = \frac{5}{3}$ .

Siehe auch

Einzelnachweise

↑ A. Sommerfeld: Vorlesungen über Theoretische Physik, Bd. V: Thermodynamik und Statistik. Nachdruck Harri Deutsch, Thun 1988, S. 31.

Weblinks

Lern-Modul zu adiabatischen Prozessen in der Atmosphäre

Thermodynamische Zustandsänderungen

adiabatisch | diabatisch · isenthalp · polytrop: isobar | isochor | isotherm | isentrop

[1] A. Sommerfeld: Vorlesungen über Theoretische Physik, Bd. V: Thermodynamik und Statistik. Nachdruck Harri Deutsch, Thun 1988, S. 31.

[1]