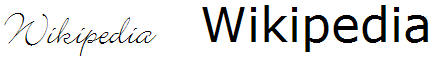Schriftgrad
Details:
1. Punze
2. Schriftbild
3. Fleisch
4. Konus
5. Achselfläche
6. Schriftkegel
7. Signatur
8. Gießrille
Abmessungen:
a Kopf
b Schulterhöhe
a+b Schrifthöhe
c Dickte
d Kegelhöhe
Die Begriffe „der Schriftgrad“, „das Schriftsatzmaß“ oder „die Kegelhöhe“ (auch „Kegelstärke“) bezeichnen in der Typografie ein Maß für die Größe einer Schrift. Der Kegel (im Bild #6) ist im Bleisatz der Körper, der das etwas kleinere, spiegelverkehrte Abbild des Buchstabens (#2) trägt. Die Kegelhöhe (Strecke d) bezeichnet die Höhe der Bleikegel. Da die Kegel etwas höher als die Buchstaben sind, ist die Kegelhöhe oder der Schriftgrad immer etwas größer als die Summe aus Ober-, Mittel- und Unterlänge und damit größer als die tatsächliche Buchstabengröße.
Für den Schriftgrad werden verschiedene Maßeinheiten verwendet und meistens als „Punkt“ bezeichnet. Diese Maßeinheiten werden bei Druckerzeugnissen nicht nur für den Schriftgrad, sondern auch für Zeilenabstände und ähnliches verwendet.
Festgeschrieben sind die Maße in der DIN 16507-1 (aktuell Stand September 1998).
Das Messgerät für in Punkt anzugebende Größen ist das Typometer.
Typografische Begriffe, optischer Ausgleich
Wie man im obigen Bild sehen kann, ragen manche Buchstaben über die verschiedenen Längen hinaus.
Häufig wird aus ästhetischen Gründen ein optischer Ausgleich vorgenommen. Zum Beispiel werden runde Buchstaben wie „a“ und „o“ oft etwas tiefer gestellt, damit sie ins Gesamtbild der Schrift passen.
Vergleich verschiedener Schriftarten
Im obigen Beispiel werden die Schriftarten Bickley Script und Verdana mit einem Schriftgrad von 36 pt nebeneinander gestellt. Aus Gründen wie etwa Schriftdicke, Mittellänge, Buchstabenbreite vermutet man nicht, dass die beiden Schriften den gleichen Schriftgrad haben. Doch wie das nächste Bild zeigt, ist dies tatsächlich so.
Der Schriftgrad sagt also nur aus, wie hoch die Schrift ist, aber nichts darüber, wie groß die Schrift empfunden wird.
Die Einheiten des Maßsystems
Das französische Punkt-System
Der Punkt (p) ist die Grundeinheit zur Angabe von Schriftgrößen.
Das erste typographische Punktsystem wurde von Sébastien Truchet (1657–1729) konzipiert. Sein Punkt betrug genau 1/1728 „pied du Roi“ (Fuß), also etwa 0,188 mm und entspricht somit genau der Hälfte des späteren Didot-Punktes.
Etwa seit 1737 verwendete der französische Drucker Pierre Simon Fournier einen eigenen typographischen Punkt. Er betrug etwa 0,345 mm, also etwa elf Zwölftel spätere Didotpunkte. Der sogenannte Fournier-Punkt wurde dann nicht weiterverwendet.
Weiterentwickelt wurde das Maßsystem Ende des 18. Jahrhunderts von François Ambroise Didot und seinem Sohn Firmin Didot.
Der Didot-Punkt, der sich dann auch praktisch in ganz Europa durchsetzte, betrug traditionell 0,376065 mm (nach offizieller Umrechnung aber etwa 0,3759715 mm). Er wird üblicherweise mit 0,376 mm angegeben und auch so verwendet (mit +0,0173 % bzw. −0,0075 %, weit innerhalb aller technischen Toleranzen). Das Grundmaß war der Fuß, das alte französische Längenmaß Pied de roi. So entsprechen 6 × 12 × 12 = 864 Didotpunkte genau einem französischen Fuß.
1975 wurde vorgeschlagen, den Didotpunkt auf 0,375 mm abzurunden. Für die Verwendung mit den existierenden Druckmaschinen ist aber eine Modifikation von mehr als einem Viertel Prozent erheblich und war daher technisch zu schwierig zu verwirklichen. Außerdem wurde zu dieser Zeit gerade auf Fotosatztechnik umgestellt, die den DTP-Punkt verwendet. So wurde dieser Vorschlag in der Praxis nie vollständig umgesetzt, obwohl oft vereinfachend ein Didot-Punkt als 3⁄8 mm angegeben werden.
Die nächstgrößere Einheit in diesem System ist das Cicero. Ein Cicero entspricht 12 Didot-Punkten. Vier Cicero wiederum ergeben eine Konkordanz.
Das amerikanische Punkt-System
Ende des 19. Jahrhunderts kam aus den USA mit der Erfindung der Linotype-Zeilengussmaschine ein alternatives Punktmaß auch nach Europa: der Pica-Punkt (pp). Die amerikanischen Drucker verwendeten einen eigenen, amerikanischen „Druckerfuß“, der recht genau 1024/1000 römischem Fuß entspricht, also etwa 303,5 mm.
Von drei konkurrierenden, fast gleichen Definitionen verabschiedete das 15. Meeting der US-Type Founders Association der U.S.A. (1886) das sogenannte „Johnson Pica“ zu genau 0,166 Zoll. Die anderen beiden Vorschläge, Nelson C. Hawks: 1200 / 7227 gleich etwa 0.166044 inch, sowie die direkte Bezugnahme auf das metrische System: 83 pica in 350 mm, also etwa 0,1660184 inch blieben unberücksichtigt.
Daher misst der traditionelle amerikanische Printer’s Point 0,35136 mm. Analog zum Didot-Punkt bildet hier ein Pica (= 0,166 inch) das nächsthöhere Schriftmaß von 12 Punkt.
Das DTP-Punkt-System
Das DTP-Punkt-System (DTP von: Desktop-Publishing) wird heute im IT-Bereich nahezu ausschließlich verwendet.
Der typographische DTP-Punkt, abgekürzt ‚pt‘ (TeX: ‚bp‘ für big point), gelegentlich auch PostScript-Punkt genannt, wurde als der 864. Teil des englischen Kompromissfußes von 1959 definiert. Er misst also exakt 1⁄72 Zoll, d.h. 0,0138 Zoll oder 0,3527 mm. Er ist zurzeit das einzig verlässliche Maß in den meisten Anwendungsprogrammen (Druckerkommunikation, Word, Photoshop etc. – CorelDraw hingegen wurde metrisch programmiert).
DIN 16507
Die deutsche Norm DIN 16507-2:1999 sieht für Schriftgrößenangaben und Zeilenhöhen im elektronischen Satz ein Modul von 250 µm vor, mit einem Submodul von 50 µm für Zwischengrößen. Dieser Modul wird teilweise auch wie eine dem Punkt entsprechende Einheit verwendet und heißt dann Quart (‚q‘), da sie einem Viertelmillimeter entspricht.
Statt der Kegelhöhe wird in DIN 16507-2 die messbare Größe der Versalhöhe zur Angabe der Schriftgröße verwendet. Dieses System hat bisher keine weite Verbreitung gefunden, allerdings unterstützen verschiedene Computertypographiesprachen (z. B. TeX, CSS, Framemaker) die Maßangabe in metrischen Einheiten.
Otl Aicher war einer der Befürworter dieses Systems und propagierte Schriftgrade, die teilweise an die traditionellen Namen angelehnt sind.
| Anwendung (Name) | q | mm | μm | dd | pt | pp |
|---|---|---|---|---|---|---|
| (Perl) | 7 | 1 3⁄4 | 1750 | 4 2⁄3 | 5,0 | 5,0 |
| Fußnote (Nonpareille) | 9 | 2 1⁄4 | 2250 | 6 | 6,4 | 6,4 |
| Tabelle | 10 | 2 1⁄2 | 2500 | 6 2⁄3 | 7,1 | 7,1 |
| Legende | 11 | 2 3⁄4 | 2750 | 7 1⁄3 | 7,8 | 7,8 |
| Zeitung (Petite) | 12 | 3 | 3000 | 8 | 8,5 | 8,5 |
| Buch, klein | 13 | 3 1⁄4 | 3250 | 8 2⁄3 | 9,2 | 9,2 |
| Buch, groß | 14 | 3 1⁄2 | 3500 | 9 1⁄3 | 9,9 | 10,0 |
| Foliant (Korpus) | 15 | 3 3⁄4 | 3750 | 10 | 10,6 | 10,7 |
| Titel (Cicero) | 18 | 4 1⁄2 | 4500 | 12 | 12,8 | 12,8 |
Tabelle der Schriftgrößen
Die entsprechenden DTP-Größen sind recht genau ein Sechzehntel kleiner als die Didot-Maße.
Überblick über das typografische Maßsystem
| Punkte | Schriftgrad-Name (Maß) | mm (Didot) | mm (DTP) | Stand der Schriftlinie in Didot-Punkten |
|---|---|---|---|---|
| 1 | Achtelpetit | 0,376 | 0,353 | |
| 1½ | Achtelcicero | 0,564 | 0,529 | |
| 2 | Non Plus Ultra (Viertelpetit) | 0,752 | 0,706 | |
| 2½ | Microscopique | 0,940 | 0,882 | |
| 3 | Brillant (Viertelcicero) | 1,128 | 1,058 | |
| 4 | Diamant (Halbpetit) | 1,504 | 1,411 | von unten 0,9 |
| 5 | Perl | 1,880 | 1,764 | von unten 0,9 |
| 6 | Nonpareille | 2,256 | 2,117 | von unten 1,4 |
| 6½ | Insertio | 2,444 | 2,293 | |
| 7 | Kolonel, Mignon | 2,632 | 2,469 | von unten 1,9 |
| Grobe Kolonel | von unten 1,4 | |||
| 8 | Petit | 3,009 | 2,822 | von unten 1,9 |
| 9 | Borgis, Bourgeois | 3,385 | 3,175 | von unten 2,4 |
| Grobe Borgis | von unten 1,9 | |||
| 10 | Korpus, Corpus, Garmond | 3,761 | 3,528 | von unten 2,4 |
| Grobe Korpus | von unten 1,9 | |||
| 11 | Rheinländer, Brevier | 4,136 | 3,881 | |
| 12 | Cicero | 4,513 | 4,233 | von unten 2,9 |
| 14 | Mittel | 5,265 | 4,939 | von unten 2,9 |
| 16 | Tertia | 6,017 | 5,644 | von unten 3,9 |
| 18 | Paragon (1½ Cicero) | 6,769 | 6,350 | |
| 20 | Text | 7,521 | 7,056 | von unten 3,9 |
| 24 | Doppelcicero (Zweicicero) | 9,026 | 8,467 | von unten 5,9 |
| 28 | Doppelmittel | 10,530 | 9,878 | von unten 5,9 |
| 32 | Doppeltertia (Kleine Kanon) | 12,034 | 11,289 | von unten 7,9 |
| 36 | Kanon (Dreicicero) | 13,538 | 12,700 | von unten 7,9 |
| 42 | Grobe Kanon | 15,795 | 14,817 | |
| 48 | Kleine Missal, (Konkordanz) | 18,051 | 16,933 | von unten 11,9 |
| 54 | Grobe Missal | 20,308 | 19,050 | |
| 60 | Sabon (Fünfcicero) | 22,564 | 21,167 | von unten 15,9 |
| 66 | Grobe Sabon | 24,820 | 23,283 | |
| 72 | Sechscicero | 27,077 | 25,400 | von unten 17,9 |
| 84 | Siebencicero | 31,589 | 29,633 | von unten 19,9 |
| 96 | Achtcicero | 36,102 | 33,867 | von unten 23,9 |
Ab einem Schriftgrad von 4 Punkt gilt die „Deutsche Normalschriftlinie“. Die Unterscheidung „Grobe“ vor dem Schriftnamen weist oft auf eine Absenkung der Schriftlinie hin, um ein etwas größeres (groberes) Schriftbild auf einem gleich hohen Kegel unterzubringen.
Die Schriftgrade in anderen europäischen Ländern hatten mitunter andere Namen, gleiche oder ähnliche Bezeichnungen galten für andere Schriftgrade. Ab der „Kanon“ (36 Punkt) aufwärts bezeichneten selbst in Deutschland die Namen nicht immer dieselben Schriftkegel. So findet man „Kanon“ für 32 und 36 Punkt, „Grobe Kanon“ für 40 und 42 Punkt, „Missal“ gar für 48, 54 und 60 Punkte. „Sabon“ und Bezeichnungen größerer Grade standen immer für verschiedene Kegelhöhen.
In der Tabelle stehen die gebräuchlichsten Namen zuerst.
Literatur
- Jan Tschichold, 2001: Erfreuliche Drucksachen durch gute Typographie, Kapitel Das typographische Maßsystem. Augsburg: Maro, ISBN 3-87512-413-8, ab Seite 53
- Claudia Runk, 2006: Grundkurs Typografie und Layout, Abschnitt 1.7: Typografisches Maßsystem. Bonn: Galileo, ISBN 3-89842-406-5, Seiten 79 und 80
- Eberhard Dilba: Typographie-Lexikon und Lesebuch für alle, 2. Auflage, Books on Demand, Norderstedt 2008, ISBN 978-3-8334-2522-6, Seiten 130−132
Weblinks
- Typographischer Punkt in: Typolexikon.de.
- Messen von Schrift, Information auf Webseite der Firma Adobe.
- Typographie-Lexikon von Eberhard Dilba (pdf-Datei), Stichwort: Namen der Schriftgrade, Schriftgrad, Typographisches Maßsystem