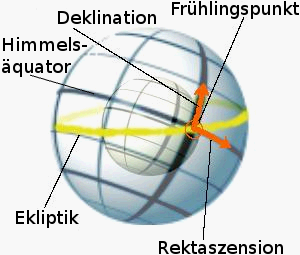
Äquatoriales Koordinatensystem
Als äquatoriales Koordinatensystem bezeichnet man zwei in der sphärischen Astronomie verwendete geozentrische Koordinatensysteme auf der Himmelskugel, das rotierende und das ortsfeste äquatoriale Koordinatensystem. Die Bezugsebene ist in beiden Fällen die Ebene des Himmelsäquators. Bezugspunkt auf dem Himmelsäquator ist beim rotierenden System der Frühlingspunkt, beim ortsfesten System der Schnittpunkt zwischen Himmelsäquator und Meridian des Beobachtungsorts.
Beschreibung
Die Position eines Objekts am Himmel, also auf der gedachten Himmelskugel, in deren Mitte sich die Erde befindet, wird durch zwei Polarkoordinaten von der Erde aus angegeben:[1]
1. Frühlingspunkt als Bezugspunkt:[2] Für Beobachter auf der Erde dreht sich der Sternenhimmel mit dem Frühlingspunkt täglich einmal um die Erde. Deshalb wird von einem rotierenden System gesprochen.
- Deklination $ \delta $ (Winkelabstand von der Äquatorebene; positives Vorzeichen für die Nordhalbkugel)
- Rektaszension $ \alpha $ (Winkelabstand vom Frühlingspunkt; ein Stern mit größerer Rektaszension wandert später durch den Meridian als einer mit kleinerer Rektaszension)
2. Meridianschnitt des Beobachters als Bezugspunkt: sogenanntes ortsfestes System (solange der Beobachter ortsfest ist)
- Deklination $ \delta $ (Winkelabstand von der Äquatorialebene)
- Stundenwinkel $ \tau $ (Winkelabstand vom Meridian, nach Westen von 0° aus zunehmend, nach Osten von 360° aus abnehmend)
Siehe auch
- Ekliptikales Koordinatensystem: Bezugsebene ist die Ebene der Ekliptik.
- Die Umrechnung zwischen den verschiedenen astronomischen Koordinatensystemen ist im Hauptartikel Astronomische Koordinatensysteme beschrieben.
Anmerkungen
- ↑ Da die Erde im Vergleich zur Himmelskugel unendlich klein ist, kann jeder Punkt auf der Erdoberfläche als Mittelpunkt der Himmelskugel betrachtet werden.
- ↑ Der Frühlingspunkt verschiebt sich durch die Präzession langsam gegen den Sternenhimmel, was bei gegenwartsfernem Gebrauch zu beachten ist.